Философская геометрия. Корень из двух.

Эта статья - продолжение первых двух.

Итак, начиная с древних греков, хотя скорее еще раньше, люди пытались найти в природе паттерны и закономерности. Было развито мнение, что в многоликом мире существует нечто неизменное, причем существует во всех вещах. Ученые искали это неизменное и натолкнулись на идею пропорций. Делая различные построения, геометры раз за разом встречали иррациональные отношения сторон в пересечении сторон прямоугльников, окружностях, пятиугольников и других фигур. Это впечатляло. Иррациональные числа стали считаться священными. Некоторые видели в них проявление божественного вмешательства. Некоторые - самого бога.

Я попробую представить как мыслил древний человек. Возможно, что создавая произведение искусства, основанное на числе ?2 ход его мыслей был примерно таким:

Корень из двух является символом природного роста. Визуальное представление геометрической прогрессии показывает как ничтожный объект может вырасти до гигантских размеров за короткое время. Корень из двух - это то неизменное, что находится в основе этой прогрессии. В этом росте - сила данного числа.

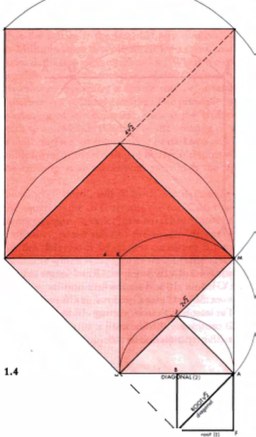
Но что такое рост? Что вообще такое процесс творения и как ничтожное может развиваться и становиться большим? Давайте представим себе точку.

Само по себе - это ничтожество. Это сущность, присутствующая в одном измерении, но в то же время, в ней заключена огромная энергия. Давайте высвободим ее.

Что дальше? Нам нужен прорыв. Откроем для себя второе измерение. Построим квадрат ABCD

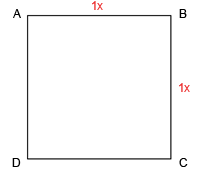
Теперь, откроем новые формы движения. С центром в точке С радиусом CB давайте проведем дугу.

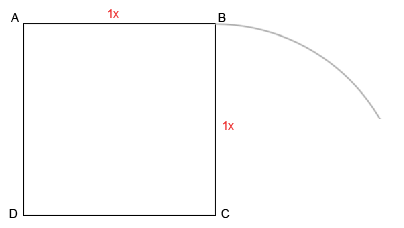
Найдем новые пути движения. Соединим AC и проведем перпендикуляр CE. Длина AC - это ?2 - фактор, удваивающий измерение.

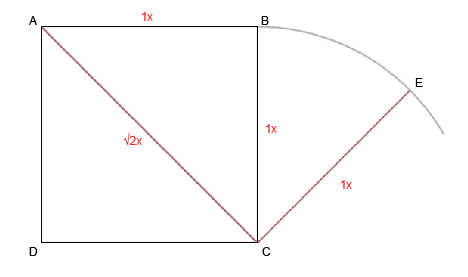
Давайте проведем линию AE

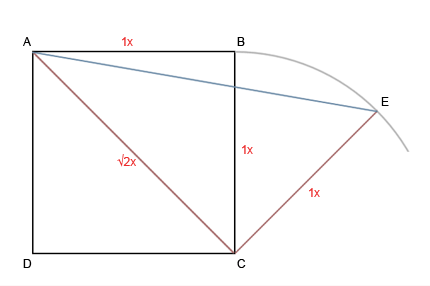
Теперь, симметрично отразим наши последние построения.

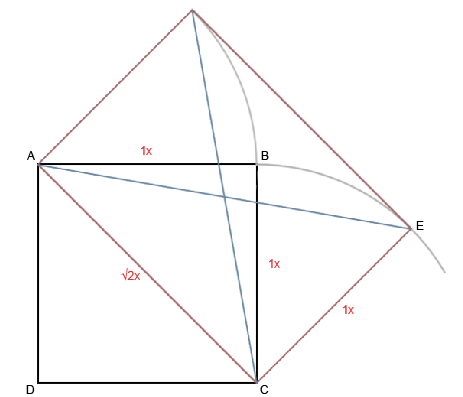
Теперь взглянем на них подробней.

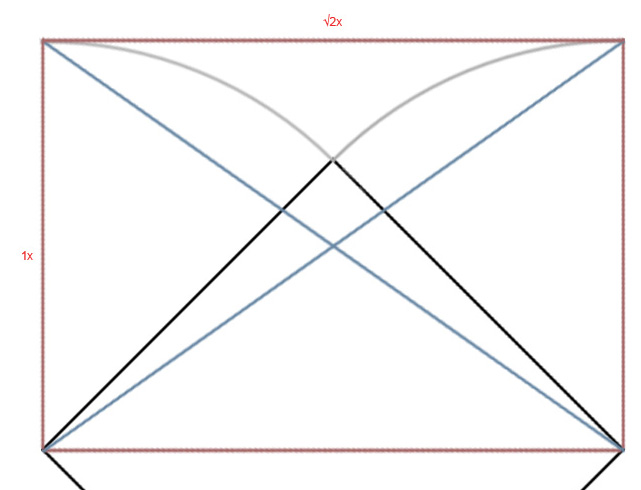
Ну что же, форма рождается сама собой.

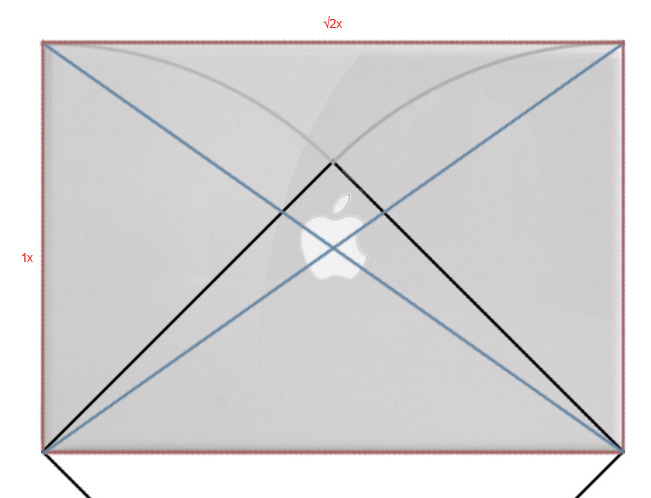
Давайте откроем ноутбук. Нам как-то нужно расположить кучу функциональных элементов, которые он имеет. Как их разместить? Очень просто. Мы только что нарисовали естесственную и красивую сетку, имеющую в основе могучую силу символа роста. Используем ее.

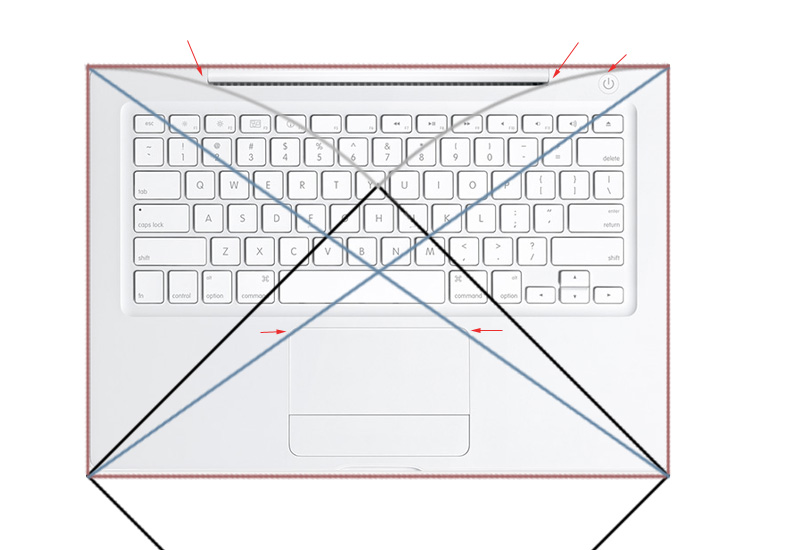
MacBook - это без сомнения очень красивое произведение дизайнерского искусства. Персонально мне нравится красота вот этого элемента.

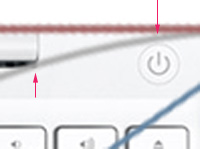
Конечно, сетка расположения всех элементов на макбуке гораздо сложней, и это мы даже не пытались выходить в третье измерение. Однако, глаз все равно улавливает некоторые закономерности.

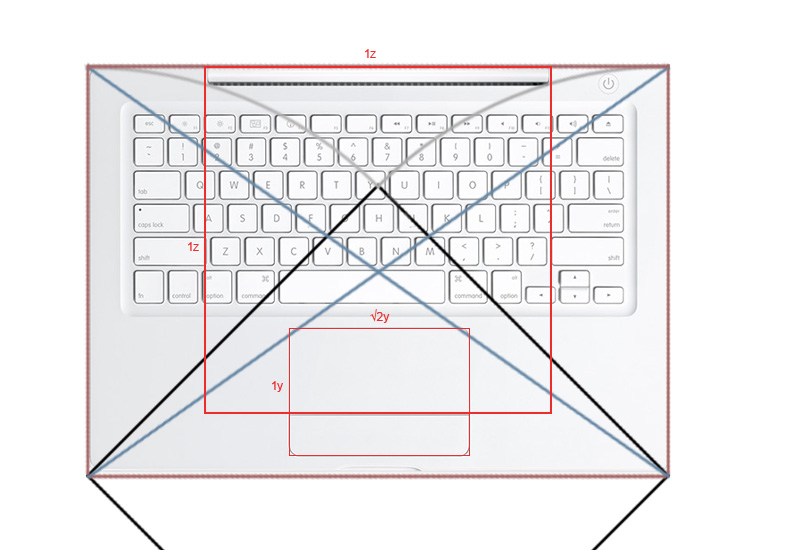
Итак, мы увидели как геометрическая философия может быть применена к промышленному дизайну. Я не претендую на какое-то открытие, или откровение в области дизайна. Модульные сетки - обыденное явление. Я хотел попробовать сделать иллюстрацию того, как работает человеческий мозг. Размышляющая мысль ветвится как корни дерева в разных направлениях. Когда корни этого дерева достигают воды - это решение задачи. Когда они образуют паттерны - это красота.

Но этой мысли вытекает следующая. Природа создала мир, удивительно гармонично взаимодействующий друг с другом. Может ли человек сделать то же со своими творениями? И как сделать из этого профит?

Размеры макбука близки к листу формата A4. Стороны такого листа относятся как ?2 / 1. Пропорциональность можно геометрически проверить проведя диагональ между противоположными углами предмета. Если второй предмет "встанет" на диагональ - он пропорционален первому.

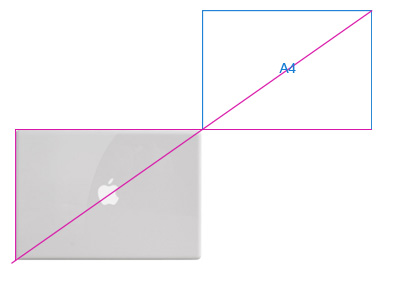
Пропорциональность продуктов компании ведет к тому, что их становится легко использовать в рекламных материалах. Расположившись в ряд на рекламе или на витрине, они гармонируют друг с другом. Несколько продуктов начинают казаться одним целым, единым, входящим в одну систему.

Эппл, кстати, поступил просто. И новый макбук и старый белый, и макбук эйр у них одного размера. А MacBook Pro максимально приближен в к ним в пропорциях, хотя и не полностью.

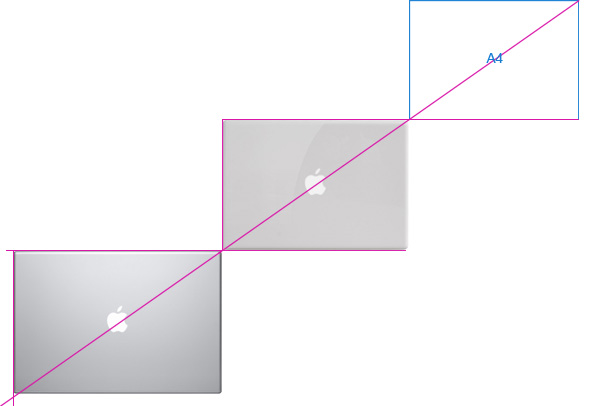
А как же остальные? В конце концов на планете полно гениальных дизайнеров. Давайте возьмем Sony Vaio - отличные популярные красивые ноутбуки. Как у них со взаимодействием друг с другом? Создают ли они чувство целого?

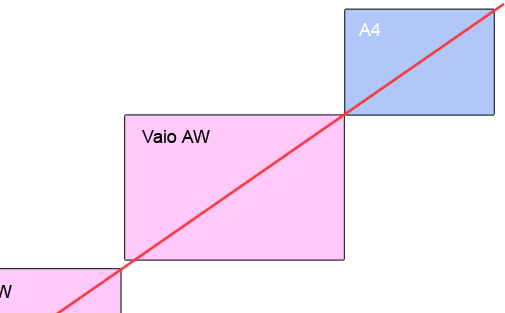
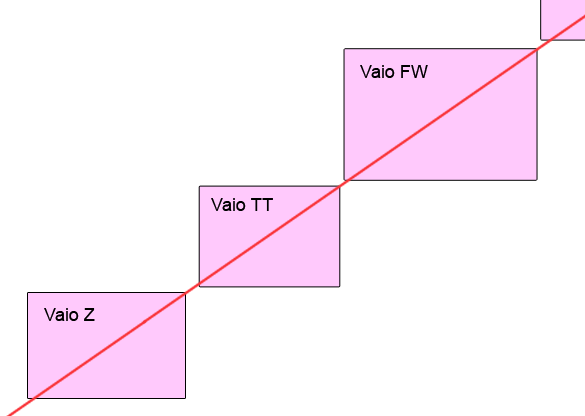
Пиксельные размеры прямоугольников пропорциональны реальным размерам ноутбуков, которые я взял с сайта производителя. На таком масштабе не очень хорошо видно, но посчитав числовые значения отношения их сторон, можно увидеь что нет, они не пропорциональны друг другу.

Давайте возьмем другие хорошие ноутбуки - Toshiba. Я нарисую здесь две штуки. Этого достаточно для общей иллюстрации положения дел.

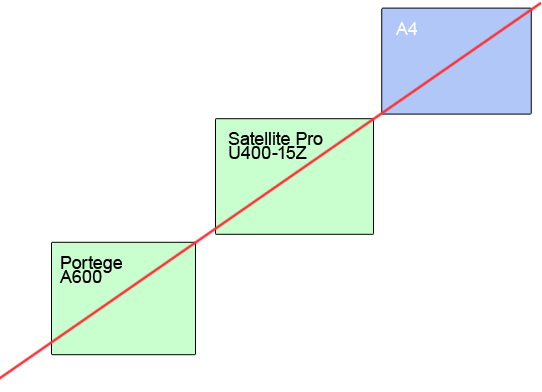
Это всего лишь тест на соблюдение пропорции, но если мы сравним сайты трех компаний, то общее впечатление о них будет примерно таким же. Если Apple целостен, а Sony хорош, то Toshiba повергла меня в легкое уныние.

Когда в нескольих вещах присутствует нечто одно неизменное, оно производит красивую сбалансированную систему из многих вещей. Это можно использовать в дизайне, рекламе, маркетинге и других видах человеческой деятельности. Сам образ мышления человека работает подобным способом, причем в двух направлениях. В начале статьи я показал как из ничтожно малого природа и человек могут построить большое. В конце статьи я показал как продукты этих построек могут восприниматься человеком на неосознанном уровне. Если он находит в них путь обратно к малому, то может быть это значит, что он нашел красоту?