Дизайн вокруг
|
Дизайн — это потрясающая многогранная вещь. Замечали, что айпод построен по принципу золотого сечения? Знаете как соединяется графический дизайн и психология восприятия человека? А как семиотика используется в юзабилити? Слышали про Тафти? Дизайн — вокруг. В этом блоге я исследую дизайн и пишу о своих находках. |
Откуда берутся ассоциации к словам: феномен Такете и Малума
Есть такая штука в мозге человека: когда мы слышим любое слово, мы его представляем. Даже когда мы читаем это слово - все равно в голове рождается смутный образ. Интересные вещи получаются когда перед нами незнакомый термин или вообще бессмысленная белиберда. Так вот, в зависимости от написания этого слова мы представляем его либо угловатым и жестким, либо мягким и округлым.
Этот феномен полезно использовать в идентике. Что вы представляете когда слышите "Билайн"? А "МТС"? Соответствует ли графический знак этих компаний тому, что представляет человек, который никогда их логотипов не видел?
Я уже писал в этом блоге на эту тему. В этой записи я выкладываю PDF-версию, красиво оформленную и готовую для печати. Ну или для закачки в ваш айпад :)

Аннотация:
Все люди почти одинаково связывают бессмысленные слова с бессмысленными фигурами. В статье описано как использовать эту особенность при создании логотипов.
32 с., М, 2009
ПэДэЭф:
sp2-maluma.pdf (344 Кбайт)
Распространяется свободно.
Присылайте комментарии вот сюда или мне на емейл, плз
Философская геометрия. Книга
Эгегей! Наконец-то оформил мою первую книжицу. Встречайте: труд, порвавший Хабрахабр в пух и прах. Подрыв устоев, накал страстей.

Аннотация:
В религиозных иконах, картинах и памятниках архитектуры широко используются иррациональные числа. В статье показана связь между этими числами и современной продукцией Apple.
32 с., М, 2009
Разворот:

ПэДэЭф:
sp1-geometry.pdf (4.5 Мбайт)
Распространяется свободно.
Присылайте комментарии вот сюда или мне на емейл, плз
Передача эмоций через телефон
Anna Stahl, Kristina Hook и Petra Sundstrom в статье A Foundation for Emotional Expressivity рассказывают как они создавали интерфес для выражения и передачи другим своих эмоций.
Идея была в том, чтобы сделать программу для обмена сообщениями, в которой можно было бы указать его эмоциональную окраску. Причем, в прямом смысле.
Эмоция должна быть выражена в фоне экрана телефона на экране с сообщением. Фон должен принимать определенный цвет, с определенными анимированными фигурами на нем. То есть эмоциональность складывается из трех составляющих:
| — | Цвет |
| — | Форма |
| — | Анимация движения |
В качестве эмоциональной теории цвета авторы выбрали теорию K. Ryberg. По ней красный цвет представляет самые сильный и мощные эмоции, а синий - минимально энергетичен. Соответственно, цвета располагаются по кругу между этими двумя крайностями. Конечно, теория не кросс-культурна, но авторы на это и не замахиваются.

Для разработки фигур и анимации, представляющих эмоции были взят анализ Лабана, который говорит как разные эмоции могут выражаться языком тела актера. На этой основе были разработаны "положительные" и "отрицательные" фигуры.

Наконец, все это было объединено вместе, запрограммировано в Sony Ericsson P800 и названо eMoto.

Как и следовало ожидать, тестирование на людях показало, что в целом задуманные фигуры и цвет совпадают с тем, как это применяли тестируемые, но процент неверных с точки зрения авторов выборов был слишком велик.

Разногласия с задумкой получались в тех случаях, когда люди видели в цвете или фигуре символ. Одна девушка сказала что желтый для нее - печальный цвет, потому что он напоминает ей закат, который так печален (авторы считали это цветом радости). Другая девушка увидела в фигуре огорчения розу и это показалось ей цветом любви.
Итого, все это лишний раз подтверждает, что эмоции по большей части персонализированы и для каждого человека соединены с символами, понятными ему. Универсальных 100% работающих на всех физиологических методов влиять на эмоции через зрение вероятно все же не существует.
Вот полный текст статьи:
|
a_foundation_for_emotional_expressivity.pdf (размер 2308.17 КБ) |
Трехмерная модульная сетка
Вот cтатья Ефима Адамова "Размышления о пространственной (трехмерной) модульной сетке". Обычные полиграфские сетки отмеривают шаги в двухмерном пространстве. В этой статье автор показывает как можно в графике применять разработанную им модульную сетку, оперирующую еще и глубиной.
|
3d_grid.pdf (размер 1070.76 КБ) |
Машинистость машины
Продолжая вчерашнюю тему про дизайн станков начала XX века еще одна интересная вещь.
L. Burlingame, работавший в компании
Дело в том, что модерн модерном, но покупатели хотели иметь станки не только функциональные, но и красивые. В результате сложилось мнение, что наиболее эстетичная машина - это машина выглящая машиной. Да, все детали должны соответствовать функции, но их форма должна подчеркивать машинистость станка.
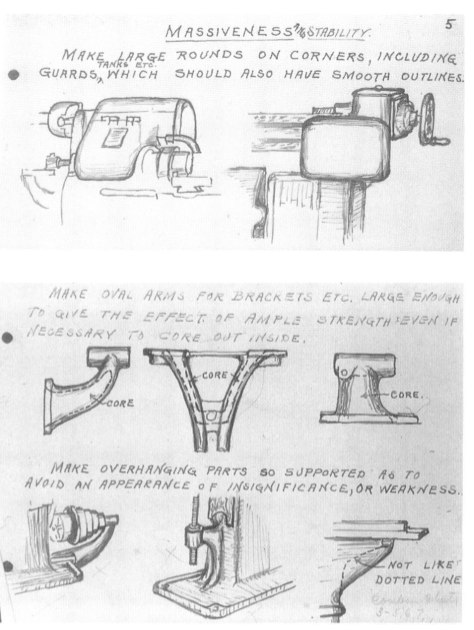
Берлингейм, как утверждает Тим Путнэм в своей статье, сделал это для придания себе статуса внутри компании, и особой ценности этот мануал не имеет. Однако интересен сам подход. "Машина" должна быть массивной и солидной. Соответственно, надо в дизайне применять такие-то приемы.
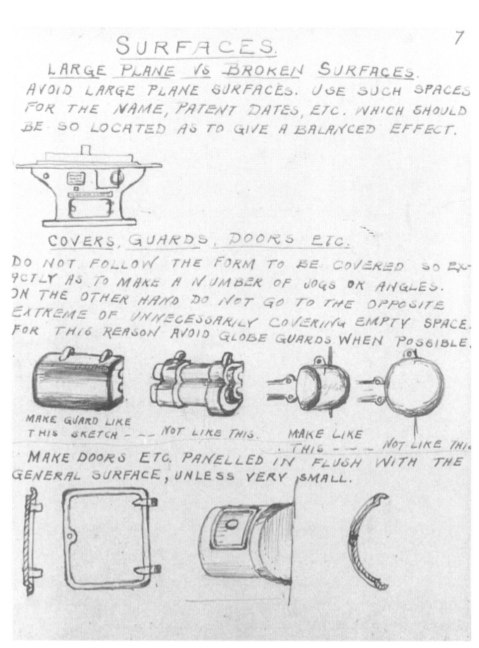
А как, например, надо оформлять новостной сайт, чтобы подчеркнуть его новостнистость? Как ни в коем случае нельзя его дизайнить? Как быть со старыми солидными изданиями, которые хотят показать, что новые технологии они используют мастерски, но только самым благопристойным джентельменским образом?
Тестирование логотипа на устойчивость
Вот логотип для международной выставки Man and his World 1967, авторства Ernst Roch.

А вот как он тестирует его на устойчивость


Вот какие тесты нужно провести с логотипом, считает Эрнст Рох:
Анализ конфигурационной жизнеспособности:
1. Обрезание части картинки
2. Взгляд с угла (тест на перспективное искажение)
Ситуационное изменение:
3. Скомканная поверхность (скажем, ваше лого будет напечатано на бумажном пакете, как в McDonalds)
4. Трехмерный барельеф с направленным освещением симулирует материальное воплощение логотипа (например, американцы любят отливать свою символику в камне и ставить перед входом в офис). Для этого нужен такой тест.
5 и 6. Манипуляции с фокусом и движением. Так будет воспринимать изображение на рекламном щите проносящийся мимо автомобилист.
Итого, если вы - заказчик, и вам делают новый фирменный стиль, не поленитесь, протестируйте логотип на устойчивость. Попросите дизайнера сделать варианты лого по этому чеклисту. Если же вы и есть дизайнер, предложите клиенту эти варианты, поразите его своим профессионализмом :)
PS: Кстати, вы обращали внимание, что первый айфон безошибочно определяется по любому его куску? Тестирование айфона, мммм....
Инструкции для дизайнеров в Англии XVIII века
В 1991 в журнале Journal of Design History вышла статья Design Instruction for Artisans in Eighteenth-Century Britain авторства Anne Puetz. Вот некоторые мысли из нее.
В 18 веке в англии был выпущен ряд книг и начали развиваться дизайнерские общества, цель которых было научить местных производителей делать предметы роскоши, не уступающие в качестве злейшим конкурентам - французскому импорту.

Для обучения дизайнеров существовали, во-первых, каталоги готовых рисунков. Ремесленники брали картинки из таких книг, как, например The Ladies Amusement, Or Whole Art of Japanning Made Easy, Robert Sayer, 1762. Техника оформления работ сводилась к копипасту, а ценностью являлся вкус отбирающего и арранжирующего картинки.

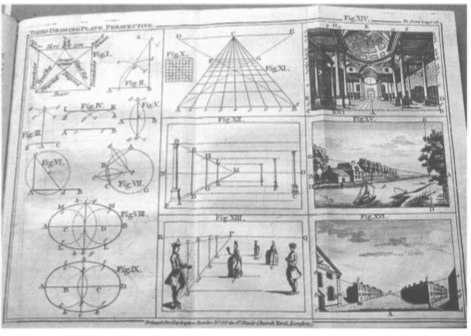
Во-вторых, имело место мнение, что дизайнеру все-таки нужно уметь рисовать, поэтому были выпущены такие пособия, как, например книга составлению орнаментов, The Principles of Ornament, or the Youth's Guide to Drawing of Foliage, Matthias Lock, 1746. А так же такие недорогие доступные книги как Artist's Assistant, Carington Bowles, где в краткой форме давались основные принципы геометрии, композиции, персективы и т. д.
Реверсивные фигуры и невозможные объекты
Реверсиные фигуры
Большинство границ у нарисованных объектов относятся к только к одному из них. Исключение составляют "реверсивные фигуры". Они появляются когда картинка составлена таким образом, что неясно к какому объекту принадлежит граница, и человек видит несколько фигур, не понимая какая из них настоящая.

Невозможные объекты
Когда две границы объекта двигаются в разных направлениях, это будет создавать противоречивое восприятие. Получаются "невозможные объекты". Этот прием можно использовать в графическом дизайне для создания щекочущего мозг эффекта.

Trademark H, Norman Ives

Trademark for Conference on Planning and Design, M. Krampen
Примеры оформления сайтов, использующих динамику формы
Я уже писал про Динамику формы в графических работах. Эта статья-продолжение с дополнительными примерами.
Оформление многих сайтов представляет собой обыкновенные статичные элементы разбросанные по обкновенному статичному холсту. Однако известно, что особенно ценятся графические работы и фотографии, в которых через формы передана динамика, движение, воздействие внешних сил. Было бы круто так оформить сайт, чтобы у зрителя создавалось впечатление динамики, движения, силы. Я нашел такие примеры и рассмотрю их ниже, но сначала немножно теории, которая даст вам вдохновение.
Примеры динамики в художественных произведениях и архитектуре

Мы все каждый день испытываем воздействие физических законов и понимаем как работают самые простые из них. Мы знаем, что форму множества предметов определяют силы, которые он использует или которым противодействует.
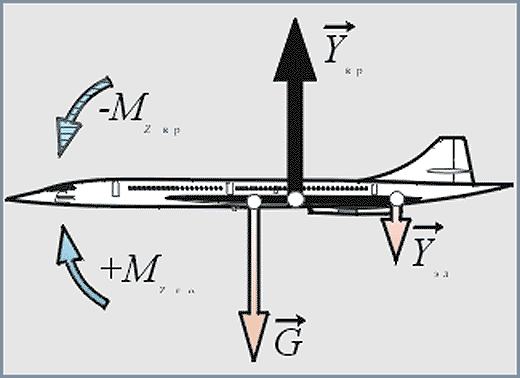
Поэтому логично, что если посетитель увидит на сайте оформление, которое скомпоновано согласно действующим на странице физическим законам, он охотней примет такую композицию элементов, будет более вовлечен в их содержание. Кроме того, дизайнер может находить неожиданные применения этим законам и эффектно преподносить их зрителю.
Далее, я рассмотрю несколько примеров оформления, где художник добивается динамики за счет намека на действующие на объект силы.
Самая основная сила, которая действует на нас всегда (если только вы не космонавт) - это сила всемирного тяготения. В форме она может быть выражена ассиметрией относительно горизонтальной оси. Тяжесь заставляет массу объекта смещаться вниз к земле. Вот эти плафоны обыгрывают этот закон.

Можно вдохновиться этим примером и попробовать нарисовать что-нибудь на его основе.

Если же предмет симметричен, масса его верхней части равна нижней, то он как бы зависает в воздухе.
НЛО отрицает гравитацию, %username%.

идея искать вдохновение в промышленных предметах может оказаться очень удачной. Их форма часто определена внешним воздействием, а так же она может быть ярко обыграна дизайнером, например вот как у этих солонок. Одну из них распирает, а во второй наверняка вакуум.

Вокруг нас всегда есть тысяча и один красивый динамичный объект. Обычная винтовая лестница обладает скрытой динамикой, спираль закручивается и ведет глаз вдоль себя, развивая бешеную скорость.

Художники давно играются с формой и динамикой.

Простое рекламное объявление может обладать внутренней динамикой. Кажется, как будто это кадр из анимационного ролика.

Но что же дизайнеры сайтов? Есть ли такие сайты, чья композиция перекликается с физическими процессами в реальной жизни?
Примеры оформления сайтов, где словно что-то движется и летит
Честно говоря, самый яркий пример оформления, который я нашел - это первая версия Яндекса.
Здесь это применено не совсем в тему, но по крайней мере все части страницы создают один вектор направления сил.
Большинство сайтов цитирует физику лишь частично.
Вот здесь развивающиеся волосы создают взмах головой.
Здесь ветер, наклоняющий ветви дерева и несущий квадратики фоток, словно листья, сдувает так же графический элемент логотипа.

Улетающая ракета дополняет рекламный текст, но на этом все и заканчивается.
Использование спирали задает дополнительной скорости бегущему человечку.
Вот на этом скриншоте плохо видно, но плашки здесь не просто висят в воздухе или стоят на какой-то поверхности, но свисают с потолка, прикрепленные за веревочку. Таким образом набившее оскомину вебдванольное отражение становится несколько более убедительным.
Наконец, сия птичка, похоже, собралась взлетать.
Итак, как показывают эти примеры оформления сайтов, идея использования физических законов имеет право на жизнь. Наиболее убедительно она будет выглядеть, когда эти силы будут использоваться не только для отдельного предмета, но и в общей композиции всей страницы. Если читателю знакомы эффектные примеры реализации этой идеи, прошу его ими поделиться.
В поисках сетки Apple
Когда я готовил статьи про философскую геометрию, я пытался анализировать композицию больших графических блоков с рекламой айподов на сайте Apple.com
Я засунул скриншот в фотошоп, обвел рамкой графический блок и поделил его пополам по горизонтали и вертикали. Для начала я проверил состоит ли сетка из прямоугольных модулей.


Похоже, что нет. Тогда я стал рисовать из разных углов блока окружности с различными, но вполне осмысленными радиусами: в половину, четверть или целую его ширины и высоты. Через точки пересечения окружностей я проводил напрявляющие (на картинках далее я оставил их только там, где обнаружил совпадения).

Совпадений оказалось достаточно, чтобы заподозрить, что дизайнеры эппла использовали похожий подход. Я не уверен на все 100%, но по крайней мере вот иллюстрация интересного способа построения модульной сетки и выравнивания объектов в блоке.
Я проверил еще картинки. Вот здесь в нижней части много совпадений, и наушники красиво легли на дугу. Умысел?
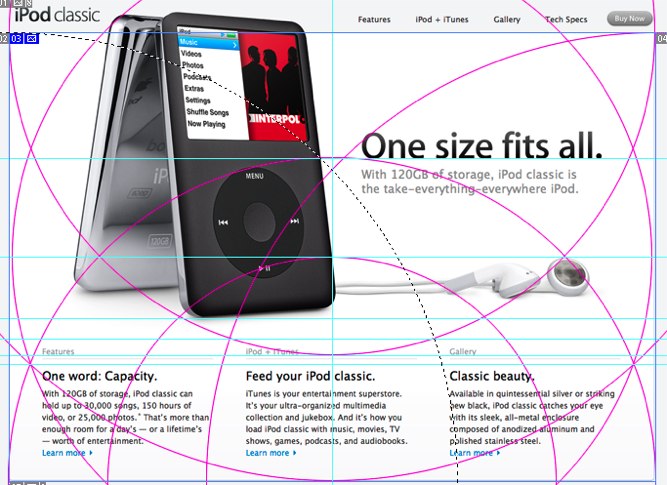
Тут в верхней части заголовки хорошо вписались в дуги. Если действительно так и планировалось, то это пример слаженной работы дизайнеров и копирайтеров. Кроме того, такая сетка идейна для картинки, в которой куча Click Wheel'ов

Здесь вроде бы ничего особенного, но у всех айподов кнопки Home подозрительно четко легли на дуги.
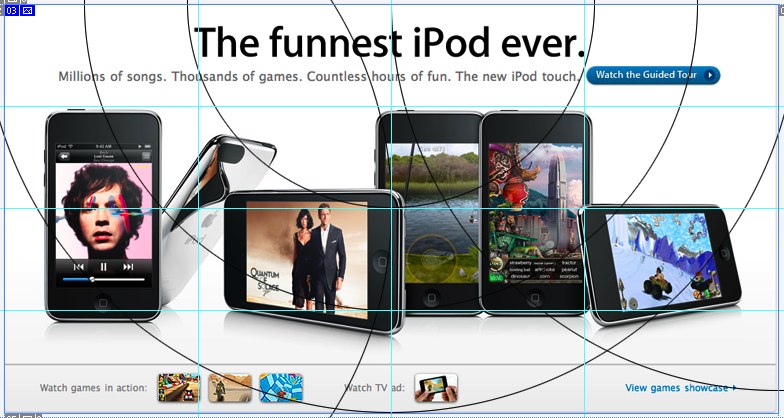
Тут я попробовал более мелкий шаг. Совпадений получилось еще больше. Особенно шаффл просто таки распростерся по точкам пересечения.

Забавно, но на русской версии я не нашел практически ничего.

Философская геометрия. Золотое сечение и корень из пяти
Упражняясь в геометрических построениях, люди древнего времени натолкнулись на идею пропорций. В различных фигурах постоянно встречались одни и те же закономерности, совпадения и паттерны. Это впечатляло.
Потом кто-то додумался измерить парочку растений, зверюшек и некоторые части тела, которые обычно от посторонних прячут. Совпадения оказались и там. Это впечатляло еще больше.
Терпеть не осталось больше мочи, самые распространенные отношения были объявлены священными. В зависимости от предпочтений, некоторые народы видели в них проявление божественного вмешательства. Некоторые - самого бога. А раз священные пропорции так часто встречаются, то подогнать под них можно все что хочешь. На их основе можно сделать символы, а символами стращать неопытные разумы паствы.
История знает массу примеров мистификаций и приписок, причем из самых благих намерений. Например, переписчики "Церковной истории народа Англов" Беды Достопочтенного приписывали к тексту куски, дабы определенные вопросы выглядели более благоприятно. А 25-28 главы VI книги "Записок о галльской войне" Цезаря по всей видимости не такие уж и Цезаря.
Так же и в символике. Надо чтобы люди чувствовали ее глубинный смысл, а сама форма не так важна. Возьми любую картинку, в ней обязательно что-нибудь золото секущееся да отыщется. Чем древнее, тем лучше. Самый древний у нас Египет, поупражняемся на нем.
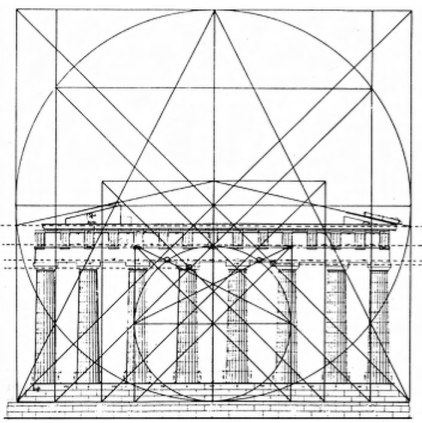
Вот схема барельефа из гробницы Петосириса, найденной в 1919 году.
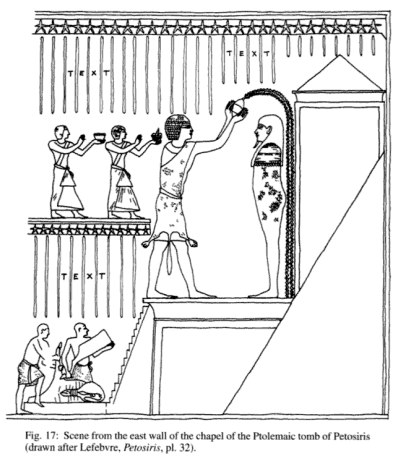
Посидев достаточное время с линейкой и циркулем, в нем можно отыскать и золотое сечение и еще кучу разных отношений.
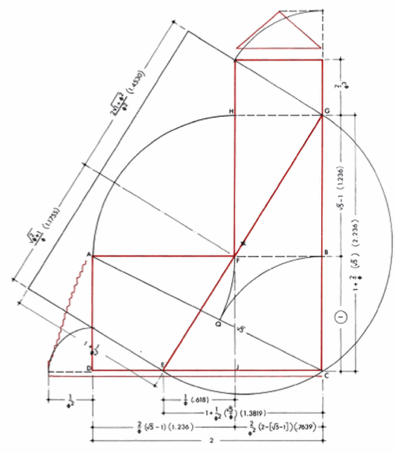
Выглядит достаточно круто, поэтому нет причин не заявить, что Египтяне знали о золотом сечении и специально все так сделали.
Мистифицировать геометрию легко и просто. Сейчас я покажу вам пару приемов.
Ну во-первых, все эти пропорции настолько древние, что все самые классные построения хорошо описаны. Открыв справочник, мы видим как самым простецким образом забубенить те самые золотые пропорции. Берем квадрат, рисуем впритык такой же и проводим диагональ AC.
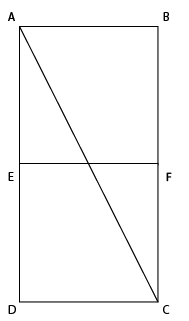
С центром O и радиусом OA строим окружность. Продляем линию FE до точки пересечения с окружностью K. Дальше можно повторить фокус с окружностью для стороны AB, но легче провести из К перпендикуляр KH, продлить AB и отметить точку пересечения H.
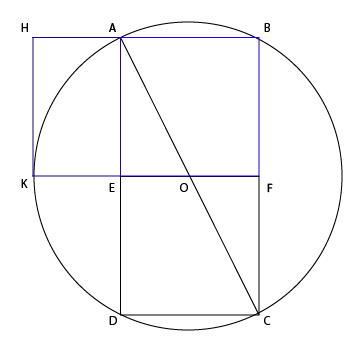
Вуаля, у нас получился "золотой прямоугольник". Отношение FE к EK такое же, как FK к FE. Что еще более офигенно, KF / FB тоже этому равно. Для краткости Греки назвали это отношение φ (Фи). Оно примерно равно 1.618 Проявляем творческое начало и делаем еще парочку пассов. Соединим углы исходного квадрата и получившегося прямоугольника. Нарисуем по образовавшимся точкам кружочек.
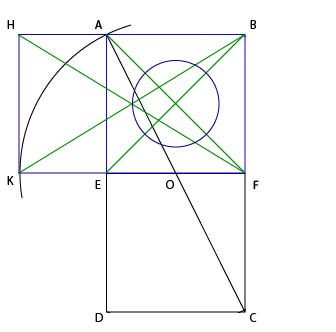
Теперь, для открытия завесы над великой тайной нам нужно найти что-то такое, чтобы вписалось в этот прямоугольник. Вспомнив как нам везло с эпплом, давайте пойдем самым простым путем и сделаем очевидное.
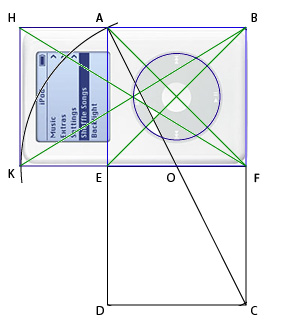
Ура! У нас получилось объявить iPod 4G священным устройством. Совершенно очевидно, что теперь его будут обязательно покупать.
Вот она - польза изучения учебников. Геометрия так долго существует, что ничего не стоит брать справочники, да классические источники, писать книжки и зарабатывать на этом много много профита.
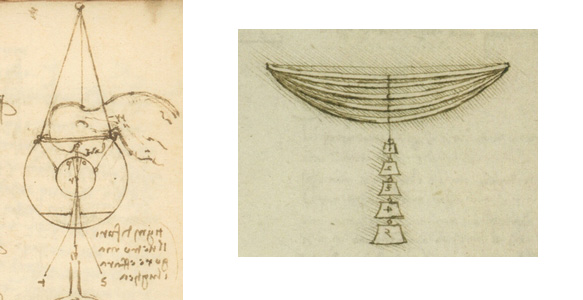
Глядишь, книжку экранизируют с каким-нибудь актером офигевшего от сценария вида, и профита станет еще на порядок больше. Можно компостировать мозг читателя, а можно компостировать мозг читателя тем как можно компостировать мозг читателя - тоже, кстати, прибыльно (ну вы понимаете о чем я). На крайняк, можно заработать кой-какие плюсы разгадав тайны арабской мозаики, связав ее... ну скажем с жуком.
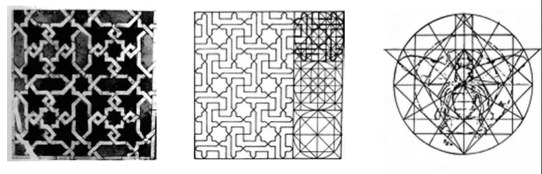
На самом деле в искусстве разумеется все дело в обычных модульных сетках и направляющих линиях, которые используют художники и дизайнеры для составления композиций. Идея настолько стара, что ее использовали даже самые древние из древних египтян.
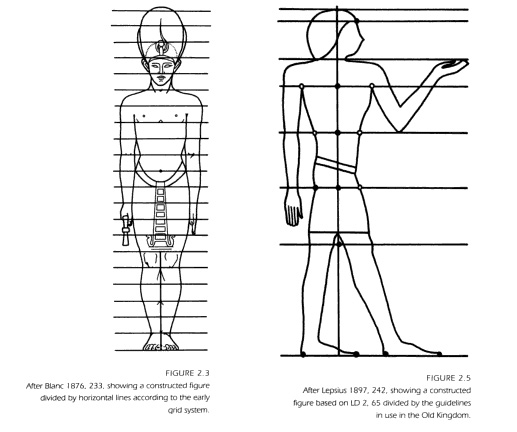
Композиции учат в художественных школах, а тех, кто учит тоже кто-то когда-то учил. Так что никакой мистики. Разве что только самый самый первый учитель что-то там напридумывал. Остальным достаточно взять какую-нибудь сетку и расставить по ней элементы.
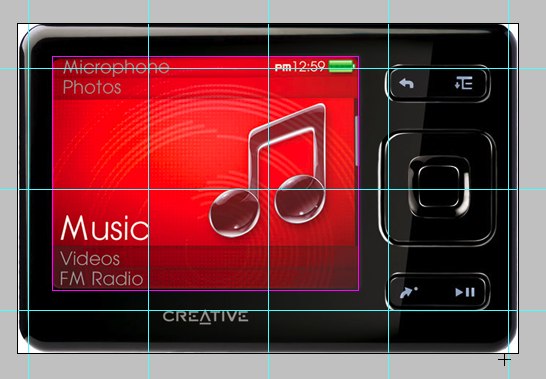
Но полуторное отношение сторон и квадратные модули - это не интересно. Нету тайны. Лучше взять что-нибудь более "сакральное". Скажем, еще одно известное отношение - ?5. У плеера Zune как раз такое.

Поглядим в справочник и посмотрим какие могут всплыть закономерности.
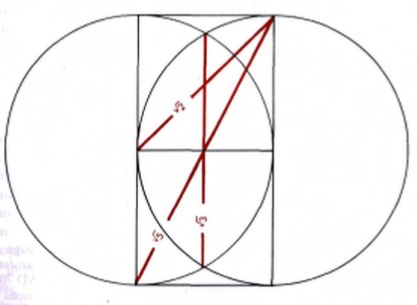
Наложим их на плеер. Хм. Ничего похожего пока нет. Попробуем перебрать все варианты.
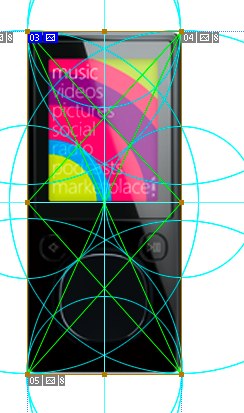
Эммм... Как-то тухло. Интересны разве что касания около центральной кнопки. Тогда возьмемся за 4иты. Притащим линейку, померим размеры элементов и попробуем найти делители.
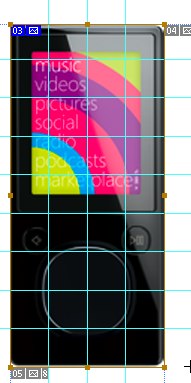
Объясняет саркоидоз и агрессивное поведение... черт, кажется не в то окно пишу. В общем, тут опять унылые квадратики, которыми мало кого запутаешь. Запороли такое хорошее начало.
Придется опять вернуться к айподам. iPod Nano 2G тоже обладает соотношением сторон ?5 / 1 Давайте снова посмотрим на схему из справочника и подумаем как прилепить его к чему-нибудь. Ага. Есть сторона ?5, которую можно втиснуть в уже готовое построение.
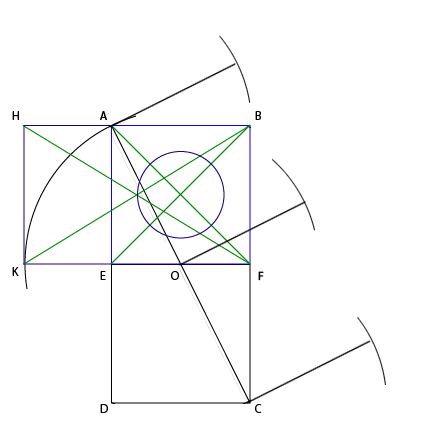
Из точек A, O и C проведем дуги с радиусом AB (так как это у нас 1x, а AC - ?5x). Из этих же точек проведем перпендикуляры к AC до пересечения с дугами. Соединим новые пересечения и вот наш айпод уже почти готов.
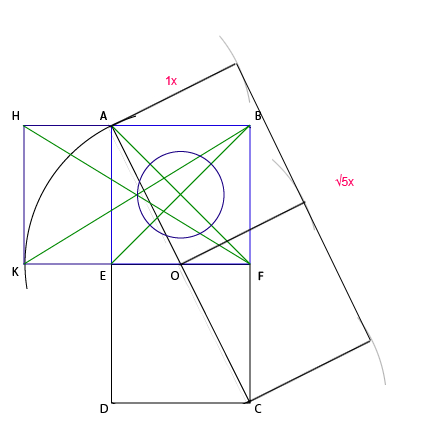
Ахайлай, махалай, абра-кадабра!
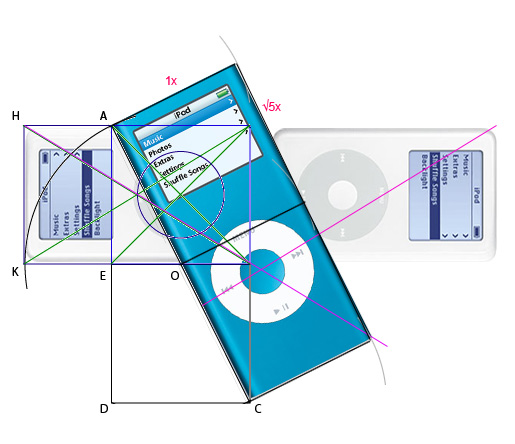
Итак, что же мы узнали? Если хочешь запутать людям голову, всегда надо использовать мистические цифры ?2, ?3, ?5 и золотое сечение — φ. С ними всегда будет больше всего "таинственных" совпадений. Есть еще много интересных вещей типа последовательностей Фибоначчи и всяких хитрых построений. Но чем проще - тем легче всех запутать, правда?

Apple совершенно точно промывают людям мозги. Ведь у них есть целый набор юного оккультиста:

Из простого квадрата можно сконструировать целый взрыв мозга, религию, философию, дихотономию добра и зла.
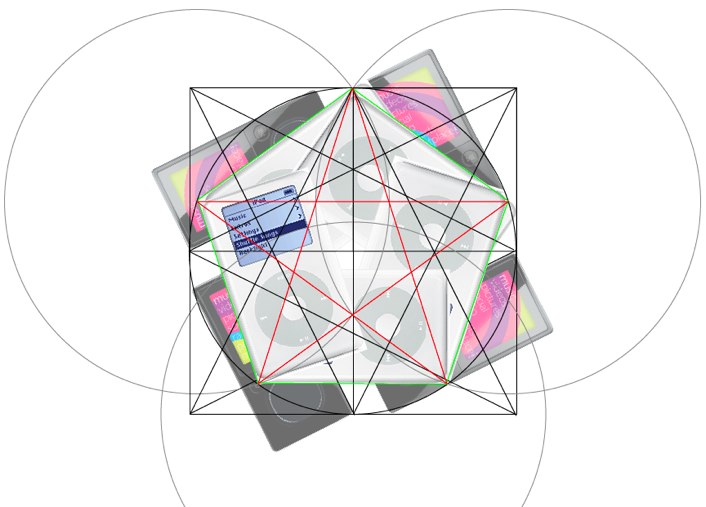
Каждый увидит здесь что захочет, включая сиськи и Микки-Мауса (еще можно звезду Давида постараться разглядеть).
А ведь с чего все начиналось:
Философская геометрия. Корень из двух.
Эта статья - продолжение первых двух.
| — | Сначала был обзор, где я говорил как древние геометры искали неизменное во всем сущем и воплощали это в произведениях искусства. |
| — | Потом была статья, где я показал как число ?3 использовалось в религиозных символах и современном всем известном предмете дизайна |
Итак, начиная с древних греков, хотя скорее еще раньше, люди пытались найти в природе паттерны и закономерности. Было развито мнение, что в многоликом мире существует нечто неизменное, причем существует во всех вещах. Ученые искали это неизменное и натолкнулись на идею пропорций. Делая различные построения, геометры раз за разом встречали иррациональные отношения сторон в пересечении сторон прямоугльников, окружностях, пятиугольников и других фигур. Это впечатляло. Иррациональные числа стали считаться священными. Некоторые видели в них проявление божественного вмешательства. Некоторые - самого бога.
Я попробую представить как мыслил древний человек. Возможно, что создавая произведение искусства, основанное на числе ?2 ход его мыслей был примерно таким:
Корень из двух является символом природного роста. Визуальное представление геометрической прогрессии показывает как ничтожный объект может вырасти до гигантских размеров за короткое время. Корень из двух - это то неизменное, что находится в основе этой прогрессии. В этом росте - сила данного числа.
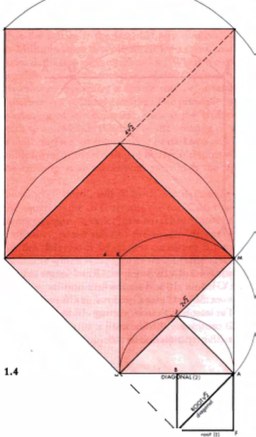
Но что такое рост? Что вообще такое процесс творения и как ничтожное может развиваться и становиться большим? Давайте представим себе точку.
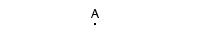
Само по себе - это ничтожество. Это сущность, присутствующая в одном измерении, но в то же время, в ней заключена огромная энергия. Давайте высвободим ее.
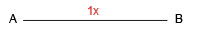
Что дальше? Нам нужен прорыв. Откроем для себя второе измерение. Построим квадрат ABCD
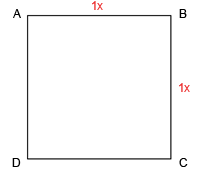
Теперь, откроем новые формы движения. С центром в точке С радиусом CB давайте проведем дугу.
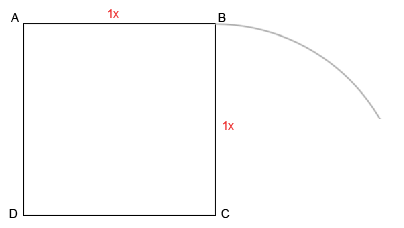
Найдем новые пути движения. Соединим AC и проведем перпендикуляр CE. Длина AC - это ?2 - фактор, удваивающий измерение.
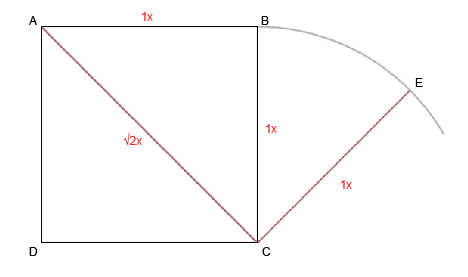
Давайте проведем линию AE
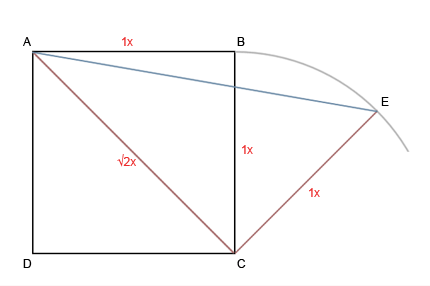
Теперь, симметрично отразим наши последние построения.
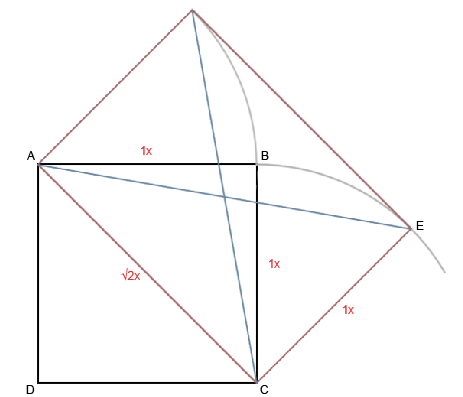
Теперь взглянем на них подробней.
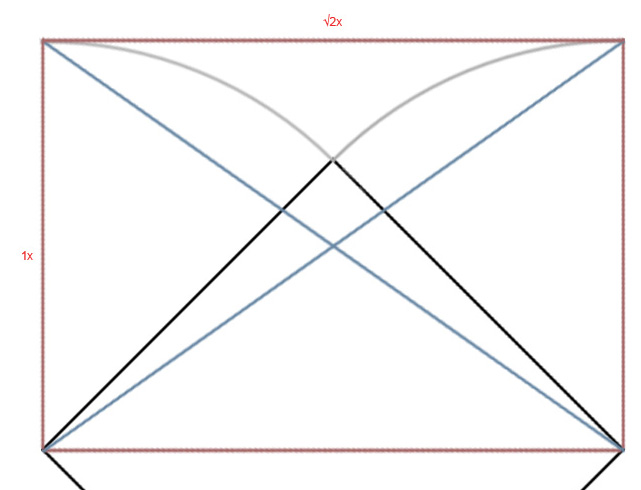
Ну что же, форма рождается сама собой.
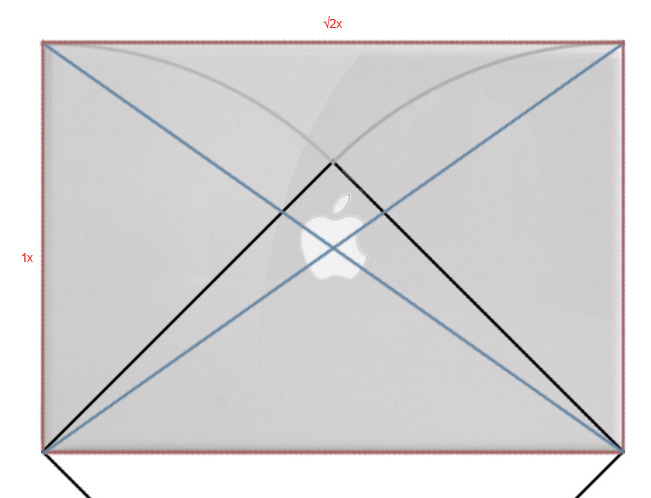
Давайте откроем ноутбук. Нам как-то нужно расположить кучу функциональных элементов, которые он имеет. Как их разместить? Очень просто. Мы только что нарисовали естесственную и красивую сетку, имеющую в основе могучую силу символа роста. Используем ее.
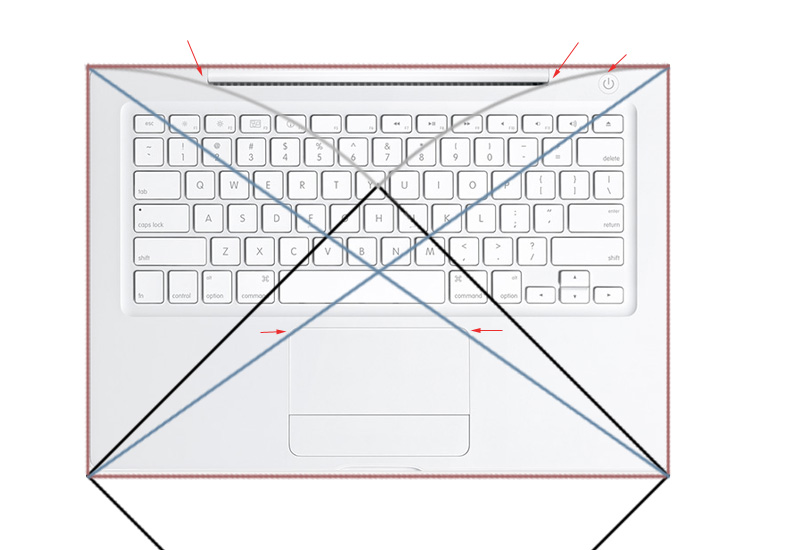
MacBook - это без сомнения очень красивое произведение дизайнерского искусства. Персонально мне нравится красота вот этого элемента.
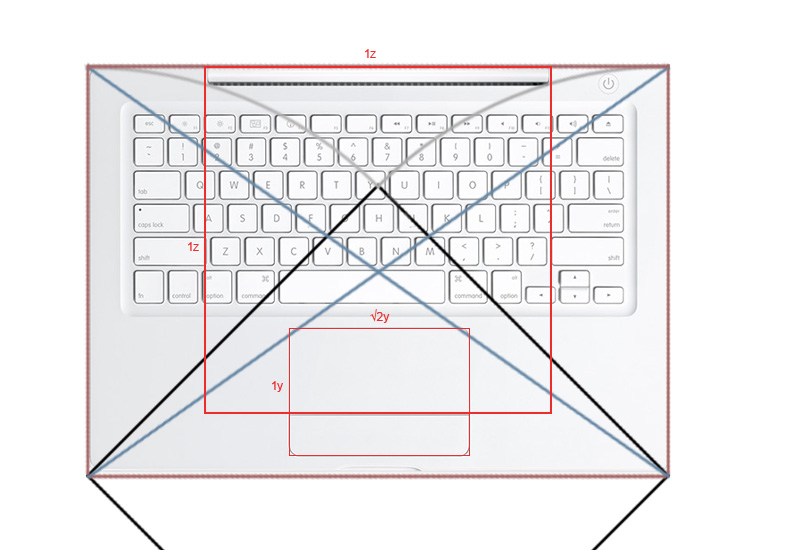
Конечно, сетка расположения всех элементов на макбуке гораздо сложней, и это мы даже не пытались выходить в третье измерение. Однако, глаз все равно улавливает некоторые закономерности.
Итак, мы увидели как геометрическая философия может быть применена к промышленному дизайну. Я не претендую на какое-то открытие, или откровение в области дизайна. Модульные сетки - обыденное явление. Я хотел попробовать сделать иллюстрацию того, как работает человеческий мозг. Размышляющая мысль ветвится как корни дерева в разных направлениях. Когда корни этого дерева достигают воды - это решение задачи. Когда они образуют паттерны - это красота.
Но этой мысли вытекает следующая. Природа создала мир, удивительно гармонично взаимодействующий друг с другом. Может ли человек сделать то же со своими творениями? И как сделать из этого профит?
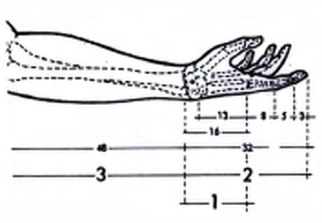
Размеры макбука близки к листу формата A4. Стороны такого листа относятся как ?2 / 1. Пропорциональность можно геометрически проверить проведя диагональ между противоположными углами предмета. Если второй предмет "встанет" на диагональ - он пропорционален первому.
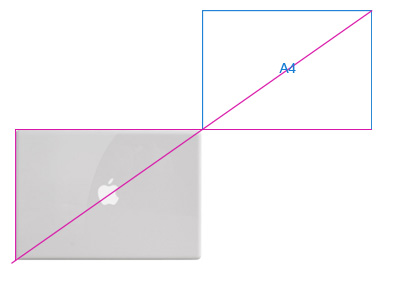
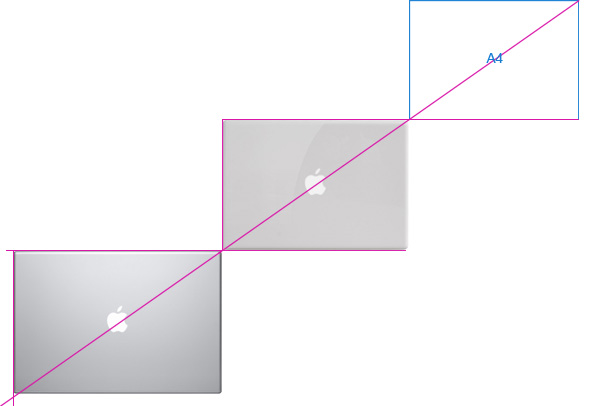
Пропорциональность продуктов компании ведет к тому, что их становится легко использовать в рекламных материалах. Расположившись в ряд на рекламе или на витрине, они гармонируют друг с другом. Несколько продуктов начинают казаться одним целым, единым, входящим в одну систему.
Эппл, кстати, поступил просто. И новый макбук и старый белый, и макбук эйр у них одного размера. А MacBook Pro максимально приближен в к ним в пропорциях, хотя и не полностью.
А как же остальные? В конце концов на планете полно гениальных дизайнеров. Давайте возьмем Sony Vaio - отличные популярные красивые ноутбуки. Как у них со взаимодействием друг с другом? Создают ли они чувство целого?
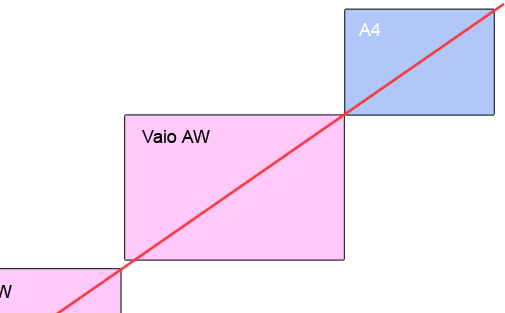
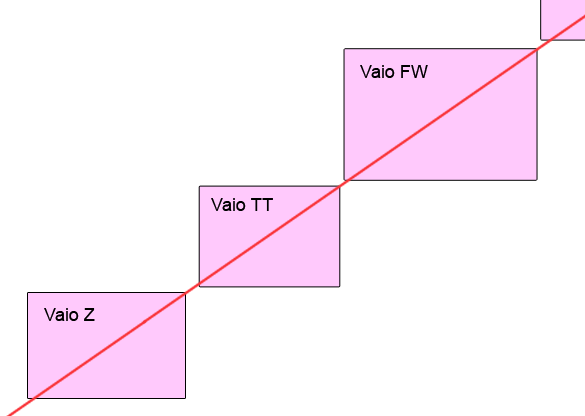
Пиксельные размеры прямоугольников пропорциональны реальным размерам ноутбуков, которые я взял с сайта производителя. На таком масштабе не очень хорошо видно, но посчитав числовые значения отношения их сторон, можно увидеь что нет, они не пропорциональны друг другу.
Давайте возьмем другие хорошие ноутбуки - Toshiba. Я нарисую здесь две штуки. Этого достаточно для общей иллюстрации положения дел.
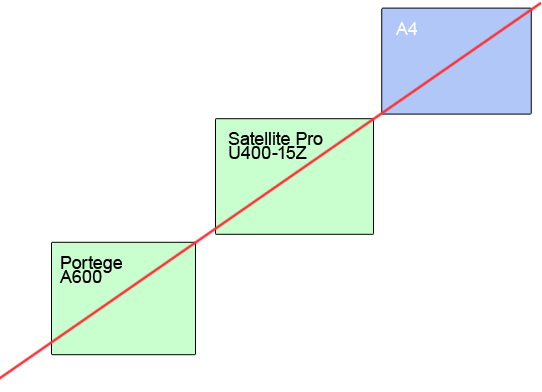
Это всего лишь тест на соблюдение пропорции, но если мы сравним сайты трех компаний, то общее впечатление о них будет примерно таким же. Если Apple целостен, а Sony хорош, то Toshiba повергла меня в легкое уныние.
Когда в нескольих вещах присутствует нечто одно неизменное, оно производит красивую сбалансированную систему из многих вещей. Это можно использовать в дизайне, рекламе, маркетинге и других видах человеческой деятельности. Сам образ мышления человека работает подобным способом, причем в двух направлениях. В начале статьи я показал как из ничтожно малого природа и человек могут построить большое. В конце статьи я показал как продукты этих построек могут восприниматься человеком на неосознанном уровне. Если он находит в них путь обратно к малому, то может быть это значит, что он нашел красоту?
Философская геометрия. Корень из трех
Я продолжаю рассказ о применении философской геометрии на практике. Прошлая часть была обзорная, она говорила о том, что многие века геометрия использовалась для поиска универсальных идеальных законов природы. Эти законы повсеместно использовались в произведениях искусства, архитектуре и духовной жизни.
Сегодня я расскажу про замечательную пропорцию "корень из трех". Я покажу ее сакральный смысл и пример из современного дизайна, который повергнет вас в шок ;)
Начнем с построения пропорции. Возьмем отрезок AB.
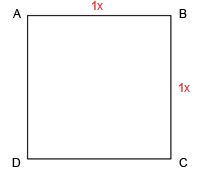
Примем его за радиус и построим окружность с центром в A.
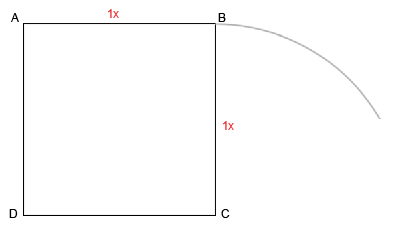
Теперь построим вторую окружность с тем же радиусом, но с центром в B.
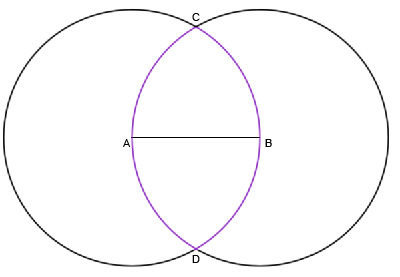
У нас получилась фигура ACBD, имеющая огромное значение для наших предков. Она называется Vescica Piscis (пузырь рыбы). Самый простой и важный пример - она давно является символом христианства.
Вот Христос вписан в эту фигуру.

Вот здесь изображено много символической рыбы.
Кстати, впервые я про это узнал, купив вот такую подвеску в Кафедральном соборе Уппсалы. Так что символ вполне используется и сейчас.

Но чем же так примечательна фигура? Давайте вернемся к построениям. Соединим точки C и D, а из места их пересечения нарисуем еще одну окружность с радиусом AB. Нарисуем прямоугольник HKLM.
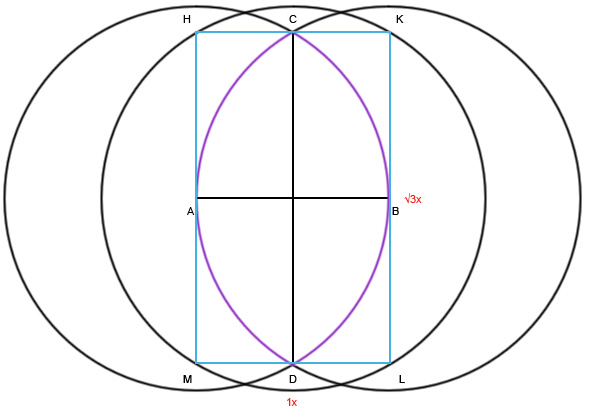
Этот прямоугольник обладает замечательным свойством. Его высота относится к ширине ровно как корень их трех (?3 / 1). Корень из трех ? это одно из основных иррациональных чисел, но основе которых строилось множество картин, зданий и просто предметов.
Но если вы думаете, что это все старо, уныло и протухло, то вы ошибаетесь. Я обещал сюрприз. Готовы? Только громко не смейтесь.
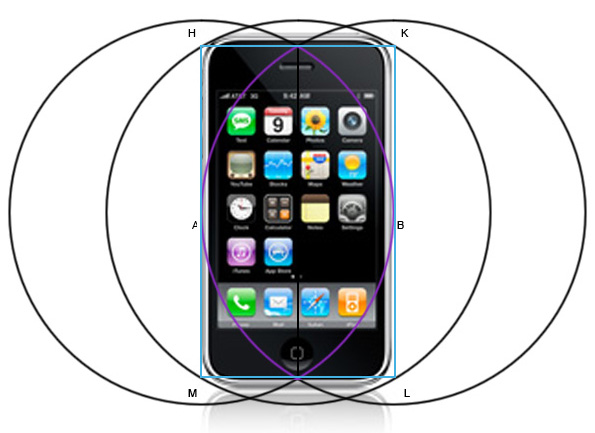
Да-да, это он. iPhone не идеально помещается в этот прямоугольник, но его размеры чрезвычайно близки. Мне кажется что это не совпадение вот почему.
Корень из трех ? это примерно 1.732050?
Отношение сторон айфона первого поколения (115x61) примерно равно 1.88524.
iPhone 3G (115.5x61.8) ? 1.8599
iPod Touch (110x61.8) ? 1.779
Смотрите, они стремятся к идеалу! Мешать им могут только тысячи технических причин.
Удивлены? Смущены? Не верите? Сейчас будет больше. Зайдем на apple.com
Хм? Что-то мне этот центральный блок напоминает. А ну ка?
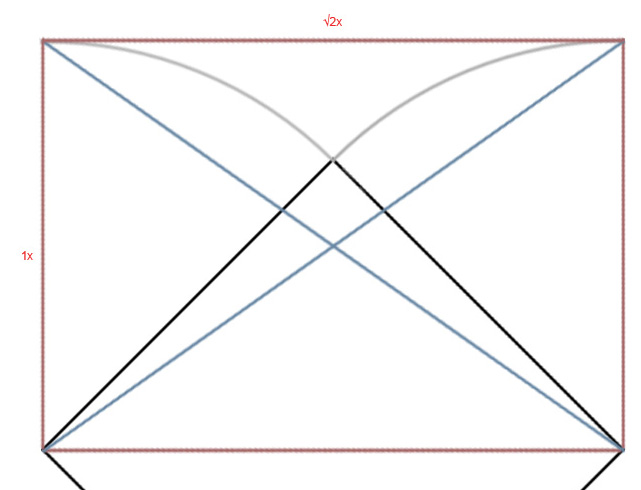
Ага! Вот вы и попались. Давайте ка посмотрим поближе.
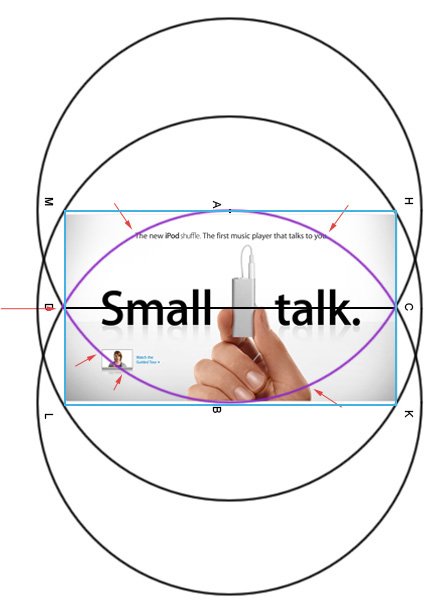
Обратите внимание как потрясающе дизайны Apple используют эту разметочную сетку. Этому геометрическому построению я даже не знаю сколько сотен лет. Оно использовалось в иконах, храмах, скульптурах. Современные дизайнеры мастерски используют его в обычных коммерческих вещах и оно продолжает безотказно работать. Их вещи покупают вопреки всякому смыслу.
Что же это мистика? Расчет? Геометрия? Философия? Нам остается только практиковаться и пытаться узнать это самим
Философская геометрия
Разливающийся Нил каждый год затапливает свои берега, а потом обнажает их вновь, оставляя открытой плодороднейшую почву. Каждый год древние египтяне должны были заново измерять свои участки земли и определять их границы. Позже, древние греки описали этот процесс и назвали его геометрией - измерением земли. Геометрия представлялась принципом установления порядка и закона в мире. Бытовая процедура стала наукой.
Платон считал, что геометрия является универсальным философским языком. Он верил, что это отличный способ погружения в философскую медитацию. Говорят, что над порогом его дома висела надпись: "Пусть не опытный в геометрии не входит в мои двери". По Платону реальность состоит из чистых сущностей или архетипичных Идей, а мы постигаем лишь их отражения.

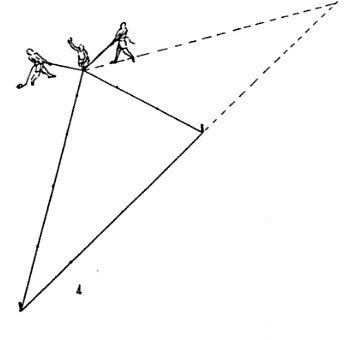
На этом изображении XVI в. геометрия представлена женщиной. Она предается размышлениям о законах и принципах устройства мира. Мужчины, изображенные вокруг нее, воплощают эти принципы в ежедневном быту. Таким образом сущности становятся объектами и практиками.
На протяжении многих веков, ученые видели мир, состоящий из геометрии и чисел. Но чисел, понимаемых не в измерительном, а качественном смысле. Поятия "двойственность" или "тройственность" не означают наличие двух или трех предметов, но значат целостные самодостаточные понятия каждое со своей силой. На этом строилась древняя философия, а на этой философии строилось изобразительное искусство.

Геометрические фигуры понимались не просто как фигуры, а как выражение этих сущностей. На этой японской каллиграфии показан процесс "сотворения", идущий от круга - "единства всего сущего" через треугольник к окончательной форме квадрата.
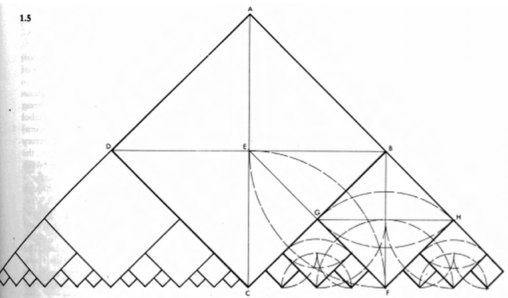
Такая философия лежит в основе многих античных произведений. Идеальные, натуральные, красивые пропорции выводились художниками, старающимися познать их в природе геометрии, чисел и "идей".
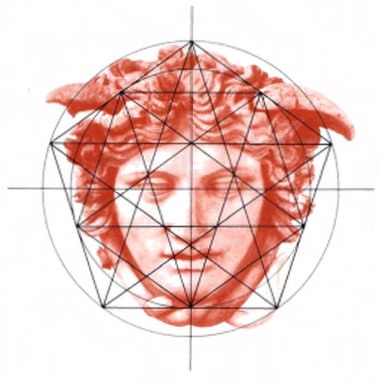
Сейчас нам тяжело понять все это. Мы воспринимаем числа совсем в другом, измерительном смысле. Нам трудно понять, почему много ученых европейцев в средние века считали ноль - числом дьявола.
Технологическая форма познания мира победила и стала общепринятой. Законы, которые выводили далекие предки, доходят до нас в виде обрывков. Философские концепции познания мира теперь являются псевдонауками, а их куски эксплуатируют всяческого вида шарлатаны.

Может быть это и к лучшему. Современная система продвинула возможности человека далеко вперед. Мы живем дольше, знаем больше и в силах грохнуть всю планету, если она нам вконец разонравится.
Однако, сама природа и ее законы, изученные в геометрии, никуда не делись. Все равно в природе существуют пропорции, иррациональные числа и различные последовательности. Например, спиральные узоры роста на подсолнухах или в расположении листьев на стебле, можно объяснить последовательностью Фибоначчи, но растению структура подобных узоров служит для усиления фотосинтеза, максимально увеличивая площадь поверхности.
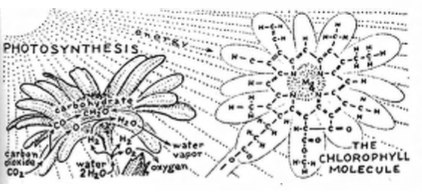
Возможно современному дизайнеру-оформителю стоит поискать такие примеры в природе и больше узнать об исследовании древних ученых для того, чтобы делать красивые и органичные вещи?
Как подобрать цвета для оформления? Посмотреть вокруг!
Эдвард Тафти в Envisioning Information упоминает об одном способе выбора цветовой палитры для оформления. Он говорит, что очень хорошо использовать цвета окружающего нас мира. Человеку должны быть приятны те сочетания цветов, которые окружают его в природной приятной обстановке в погожий день.
Я попытался развить эту идею. Можно постараться подобрать такие цвета для своей работы, чтобы они отражали палитру природы в определенном состоянии. Таким образом можно создать на своем сайте или листовке настроение зимнего утра, заката, сурового моря. Можно попробовать использовать так же урбанистические пейзажи (в конце концов мы живем в городах, а разрабатываемое оформление может стремиться передать техногенность).
Решив попрактиковаться, я взял несколько своих обычных мыльничных фотографий, потыкал в них пипеткой и покрасил получившимися цветами маленький бессмыссленный шаблон.
Вот вам погожий зимний пейзаж.

А вот немного сумрачная альпийская деревушка.

Холодный трескучий ледник.

А вот красивый закат над суровым Северным морем.

Самое обычное русское лето.

И песчаное уныние.

В общем, любой графический дизайнер лучший чем я, сможет классно подобрать цвета, и дать в своем произведении нужное ощущение реального мира. Природа - огромный источник вдохновения и то, без чего мы не можем жить. Попытаемся быть немножко ближе к ней в своей работе.
Динамика формы
Note: Я переписал эту статью и добавил примеры оформления сайтов, использующих динамику формы.
В журнале Design Quarterly No. 64 в 1966 году опубликована статья The Dynamics of Shape. В ней приводятся примеры мастерского обращения с формой. Основной тезис в том, что форма предмета - это не просто набор линий, а результат действия на предмет различных сил. Поэтому с помощью динамики формы можно подчеркивать эти силы и создавать движение в любом виде дизайна.
Например, на характер многих фигур влияет их вертикальная динамика. Сила тяжести - то, что мы испытываем каждый день, поэтому мы ожидаем увидеть ее во всем.
Страница сайта - это пространство, в котором можно установить любые свои законы. Можно ввести силу гравитации и подчеркнуть ее влияние ассиметричным развитием элементов.

А можно отменить ее. Если вертикальной силы нет, форма предмета может стать симметричной, убивая динамику. НЛО отрицает гравитацию, %username%.
статья находится в JSTOR. Это неиссякаемый источник отличных материалов. Я пришлю вам эту статью, если вы пришлете мне сначала интересную ссылку.
Основные цвета и цветовой круг
Марк Болтон (Mark Boulton) написал книгу про веб-дизайн. На сайте www.fivesimplesteps.co.uk можно узнать про нее больше, купить, а так же скачать маленький кусок.
В этом маленьком куске четко и понятно расписана теория цвета на экране.
Всем известны основные цвета:
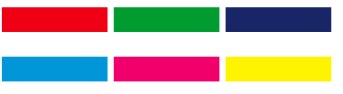
| — | Красный, Зеленый и Синий используются на экране, потому что в сложении дают белый. |
| — | Голубой, Маджента и Желтый используются в принте, потому что в сложении дают черный. |

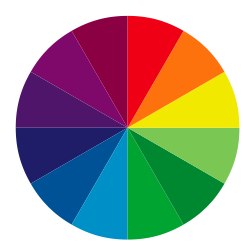
На цветовом круге цвета из разных систем расположены прямо напротив друг друга, то есть кардинально отличаются, а значит могу использоваться для контрастного различения объектов на странице
Упражнения на композицию Hajo Rose
У Отто Трейманна (см несколько постов назад) когда он учился в New Art School c 1936 по 1940 был учителем Хайо Росе (Hajo Rose). В основе его преподавания было исследование самых простых принципов дизайна: линии, цвета, структуры и методов работы. Росе особенно отмечал законы логики. Он учил студентов выбирать самый разумный и объективный из вариантов форм и материалов для решения поставленной задачи.
Одним из упражнений по композиции, которые он ставил ученикам, было иллюстрировать пространство на гладкой поверхности. Студент должен был разделить лист бумаги на девять квадратов с широким пространством слева - "для записей". Таким образом проверялась и тренировалась способность находить решения.
Трейманн шаг за шагом учился строить композиции, передающие пространство, перспективу, движение, единство и другие концепции. Он использовал различные пересечения, оттенки серого, пробовал много форм и положений объектов.
Став мастером, Трейманн мог создавать работы, выражающие мысль и идею минимальными, но очень гармоничными и красивыми средствами.

Total Identity
В 1963 году в Нидерландах образовалась группа Total Design. Ее участники Friso Kramer, Benno Wissing, Wim Crouwel и браться Schwarz намеревались ни много ни мало - заредизайнить голландский дизайн. Группа до сих пор жива, занимается профессиональным дизайном и корпоративной идентикой, основатели стали знамениты, а современная студия получила название Total Identity.

Как говорилось в прошлой заметке, Total Design развивал идеи Otto Treumann. Во многих сегодняшних работах Total Identity явно прослеживается стиль Треймана.

Что, правда, не касается их ужасающего сайта:


Otto Treumann
Отто Трейманн (Otto Treumann, 1919-2001) сыграл значительную роль в развитии послевоенного графического дизайна в Нидерландах.
Блистательными моментами в его карьере былы работы для журнала Rayon Revue, марки посвященные памяти военного сопротивления, многочисленные постеры, логотип для израильской авиакомпании El Al Israeli Airlines и для многих голландских компаний.
Трейман особо мастерски мог использовать цвет. При минимуме значений цветов и композиций он достигал чудесных результатов. Он разработал узнаваемый стиль, который доказал свою эффективность в визуальной коммуникации как в мире культуры, так и в мире бизнеса.

Он был пионером в сфере деятельности, которая позже была продолжена и отточена первыми голландскими дизайнерскими группами, такими как Tel Design (1962) и Total Design (1963).
Дизайн Трейманна функционален, ориентирован на пользователя, связывает пионеров тридцатых годов с совершенством достигнутым в профессии в шестидесятых и семидесятых.

Книгу про Отто Трейманна можно почитать на гугле:
http://books.google.com/books?id=NkST-eA7uicC&printsec=frontcover&source=gbs_summary_r&cad=0#PPP1,M1
